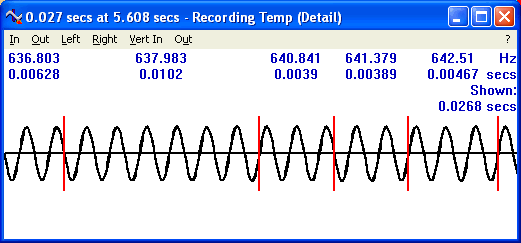
Audio Pitch Tracer - how it worksIntroThe challenge is to trace both pitch and time very exactly. Bird song is particularly challenging as many notes are very short in duration. The waveform is a simple wave (close to a sine wave). You have to get the pitch right to far better than the nearest semitone or it just doesn't sound the same, and you have to do that for notes that are very short, often a hundredth of a second or less. The methodInstead of using frequency analysis, as everyone else does in this field (as far as I know anyway), Tune Smithy (FTS) traces the waveform, and counts how many times it crosses the zero line. Here it is in action for the Loon recording:
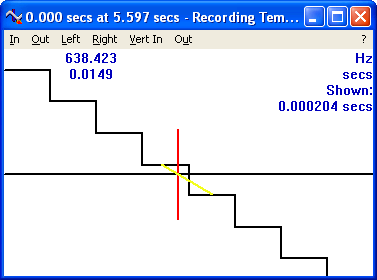
As you see, it can pick out changes in frequency over time scales as short as a hundredth of a second, or less. It is important to calculate the time very exactly - to do that you need to interpolate between samples. Here is how it does it - a close up on a single crossing:
Then to see how it works in action - let's listen to the previous loon recording slowed down to quarter speed and shifted down in pitch accordingly, so one can hear the finer nuances more easily: Here the speed is changed just by changing the sample rate of the file so the data is exactly the same.
Loon - quarter speed - WAV [5.8 MB] Midi transcription, similarly slowed down and pitch shifted. Loon Midi transcription to warm pad - quarter speed Note, a two octave pitch bend range is used for most of these midi clips, to permit large pitch glides. AccuracySurprisingly - this approach is very accuarate - because the waves are normally very close to linear at the zero crossing. The louder the note the more accurate the pitch - also 16-bit is better than 8-bit and 24, or 32 bit better still - because the larger the step from one sample to the next the greater the accuracy of the interpolation. If you do the maths, and take a typical reasonably loud 16 bit note at 441000 KHz then you can figure out a maximum error (not the average error) for the pitch accuracy. It turns out that for suitable waveforms, this method finds pitches to within a few cents (hundredths of a semitone) for a note a hundredth of a second long, and to a few tenths of a cent for notes a tenth of a second long. Transcriptions of test recordings using accurately generated sine waves bear out these conclusions. The accuracy is less if the note is very quiet. That is very accurate indeed for this sort of work, better than normal methods of frequency analysis - and sufficiently good for accurate and recognisable bird song transcriptions. It is also good enough to be of interest to even the most demanding of microtonalist composers and theorists. RequirementsSo that's the plus side. However it can't handle more than a small amount of background noise. Particularly low pitch rumbles like traffic noise tends to throw it because it displaces the waves so that often they don't even cross the zero line at all. High frequency noise tends to lead to extra spurious notes. So - you need to use clean recordings - or to clean the noise afterwards. Luckily that's not that hard to do with modern software. Particularly, it is easy to remove traffic and plane noise from birdsong recordings, at least sufficiently well so that it isn't a problem for FTS. I use Goldwave - which has good noise reduction and bandpass options. You need to reduce the noise first as much as possible - and then do a bandpass to remove all frequencies outside the region of interest. Particularly you must remove the lower frequencies. The other downside of this method is that since it doesn't examine the frequency spectrum, it normally can't handle any polyphony at all. In the case of birdsong, you may be able to handle a certain amount of polyphony. What you would do is to isolate single parts by using bandpass type filters (if necessary, work through the recording a bit at a time) - and then use FTS to transcribe each part separately, then put the resulting transcriptions together again using a midi merge. This may also work with other sounds very close to sine wave in shape. It only works with some kinds of sounds as well. For instance non harmonic timbres like bells are rather unlikely to work well. So - the requirements are -
These requirements happen to fit many bird songs very well, at least if you can get a clean recording of just the bird on its own, rather than as part of a dawn chorus or the like. It is best if the original recording is as loud as you can make it - but FTS seems to be able to handle quiet notes fairly well as well. This is for the original recording - it won't help to maximise the volume after it has been digitised, in an audio editor like Goldwave. What is important is what resolution it was recorded in originally when first converted from audio to a digital format, e.g. by your soundcard. If you can do a 24 bit or 32 bit recording, that's even better - the higher the bit resolution, then the more accurately it can interpolate to find the zero crossings. Higher resolutions help especially with quiet notes. A very quiet note at 16 bit may be recorded with only the least significant 8 bits, so is effectively only 8 bit resolution. Turn the volume up very high and you may hear that the quiet notes aren't being recorded to a very high fidelity. Similarly a very quiet 24 bit note may be 16 bit (8 bit then is very very quiet), and so on. Waves that work wellYou can tell a fair amount by looking at a recording of the sound close up in your editor, magnified so that you can see single waves. Alternatively, look at it in an oscillosope while you play the sound. If the waves look more or less like a sine wave or triangle wave or the like - just one peak to either side of the zero crossing, and cross the zero line at a steep angle - those are best of all. You are likely to be able to achieve very high levels of pitch accuracy indeed. If they have at least one main peak and don't vary much from one wave to the next, then it is likely to be possible with some tweaking of the settings. If it is complex in shape with many crossings and no main peak, but repeats more or less exactly, then it is possible, but is harder to do. Careful tweaking of the settings may be indicated. The option to search for similar waves may help. If the shape of the wave changes considerably even from each wave to the next - this is a sign of inharmonicity - and it is likely to be a tough challenge for FTS and it mightn't be able to do it at all. If the waves miss the zero line in places, and you have an effect like small ripples on bigger waves - that's a sign of low pitch noise. You need to remove that first with a low pass filter. If there are many irregularities - that's high pitch background, or noise, and needs to be removed using noise reduction, perhaps followed by a high pass filter. It is most exact with pure sine waves and the like, but can also work well with many pure harmonic timbres (wind instruments, voice, strings etc) - the closer the partials are to a harmonic series, the better. ConfusionsWhen it gets confused by noise or irregular waveforms - it may sometimes just replace them by silence, but there is also a strong tendency to find "frequencies" that simply don't exist for a human ear or a spectrum analysis. So it may find a note in the noise - and you may see nothing at all corresponding to it in a spectrum analysis. That's because it picks up on regularities in the patterning of the zero crossings rather than on frequencies in the conventional sense. It has various heuristics it uses to try and counter this - but they are only effective up to a point. If you make it's criteria too lenient then it finds extra frequencies in the noise. If you make the heuristics too severe, then it misses genuine pitches. If it seems to be confused in this way, you probably need to remove more noise. Or the waveform may be too irregular. By tweaking the settings, you can deal with a certain amount of noise and irregularity in the waveform. But beyond a certain point then the wave counting method of the Audio Pitch Tracer just can't handle it, and you will have to look for other methods. What about gongs, piano and other inharmonic instruments?As another thread I have also explored ways of improving the standard frequency spectrum type detection methods for timbres rich in partials by using information from all the partials rather than just the main one. Some waveforms such as, e.g. triangular waves are very rich in partials, but since it is a harmonic timbre, they are all in sync, and the waves are still eminently suitable for the wave counting method. But if there is just a bit of inharmonicity, for instance piano, bird song, even voice, or guitar etc on occasion - the wave counting method for the Audio Pitch Tracer may not always be able to handle the situation. So for those, I have explored methods of improving on the pitch accuracy of a more conventional frequency spectrum analysis - and although I haven't been able to get quite to the levels of accuracy of the Audio Pitch Tracer, have found some tweaks that make it possible to get into the same kind of ballpark area. The idea is to use peak interpolations. Even a three point interpolation can increase accuracy of pitch detection to much better than the usual half frequency bin size. In particular, when the peaks are known to be narrow, symmetrical, and well defined, one can do an interpolation involving not just three points, but many points to either side of the peak - and when this is possible the pitch accuracy can be increased considerably, maybe ten-fold or more even compared with the conventional three point interpolations. This often is possible for musical sounds since they do tend to have narrow and symmetrical peaks. This is highly experimental at present. It can achieve very high accuracy for medium to long notes - but is unlikely to work for notes quite as short as the hundredth of a second or shorter notes of the Audio Pitch Tracer method since the frequency bin size would be just too large to be practical. Also when using these methods it is a good idea to take a look at the frequency spectrum by eye from time to time, to check that the peaks are indeed, narrow, and symmetrical, and that the points it has found are indeed positioned at the peaks. If you want to try this out then go to the Find Notes task in Tune Smithy. Look in the Tasks folder for:
and select the Freq. Spect. method What about chords and polyphony?The wave counting method is unsuitable for most polyphonic work. It might perhaps be a useful tool for polyponic bird song (e.g. some thrushes etc can sing two notes at once) if you are able to use bandpass methods to split the original recording into two components, then analyse them separately in the Audio Pitch Tracer, then combine the result. Probalby it could be used in the same way for instruments with hardly any higher partials e.g. ocarina. Apart from that, the method is strictly monophonic, any polyphony is just regarded as noise which confuses the count. The frequency spectrum based approach however can also be used to find the pitches of notes in chords, and can work well for harmonic timbres particularly. This is possible for a recording of just a single sustained chord - you can use Tune Smithy to find the component pitches by attempting a harmonic timbre based analysis of the recording. In this way you can successfully find pitches of individual notes in chords to very high accuracy in some situations. It might be hard to tell which are separate notes and which are just additional partials belonging to the same insturment. But in the case of a harmonic timbre, then a harmonic analysis may help there. This method is likely to be used most for analysing single chords to very high accuracy. It would take a lot of work to attempt to extract single lines from a polyphonic piece. What makes polyhphonic transcription so tricky is that the human ear can very easily pick up individual instruments in a polyphonic work. Even if the timbre is new (e.g. a human voice with an unusual distinctive timbre), the ear quickly picks up its characteristics and then can trace the individual line in a larger piece. A frequency analysis will show many more spectral peaks than there are instruments (a dozen or more peaks each for some instruments), and it is amazing that the ear can pick out the individual instruments or voices so easily. Other programs exist that do attempt to transcribe polyphony with varying success - though none achieve 100% success, at least not last time I looked - they are nowhere near the capabilities of a good human transcriber. See the links page for more info, if that's what you want to do. If you are interested in finding the pitches of individual notes in a single chords to very high accuracy, however, Tune Smithy may be a useful tool - see the Sounds Harmonic Analysis. What to do nextTo continue reading about the Audio Pitch Tracer method, go on to the Music - which covers use of the method to transcribe monophonic lines on musical instruments, voice etc. Freeware / Shareware status: This feature is shareware. For details see the end of the Intro page. To find this feature after you download Tune Smithy: The program comes with a Free Test drive with all the features completely unlocked (start the test drive at any time):
|